【Day 10】人生，就是要不斷正向與反向傳遞

15th鐵人賽正向傳遞反向傳遞機器學習

許皓翔

團隊最強資工大電神

2023-09-25 23:02:12

514 瀏覽

分享至

前言

之前提到多層感知器的概念，每層的感知器會隨著層數一層一層往下傳遞，輸出的函數也會越來越複雜，而這往下傳遞的過程，就稱為正向傳遞。

在神經網路中，模型的訓練過程其實就是不斷的進行向前傳遞和向後傳遞，這兩過程是神經網路訓練的核心，所謂優化模型，就是在不斷地向前與向後傳遞中更新參數以找出最佳解。

正向傳遞 Forward Propagation

從輸入層開始，將資料通過每一層的神經元進行權重加權和激勵函數的計算，逐步計算出模型的預測結果，在正向傳遞的過程中，資料就是像這樣一層一層地，從輸入層依序通過各個隱藏層，最後透過輸出層輸出最終的模型預測值，大致步驟為：從輸出層獲取特徵 → 通過隱藏層的線性組合和激勵函數計算 → 逐層向前傳遞，最終得到輸出值。

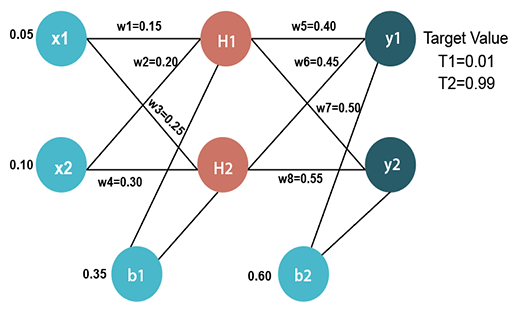
如下圖，最左邊直排輸入層的圓圈，就代表輸入的特徵神經元， $x=(x1,x2)$ 會被向右輸出到中間直排的隱藏層，經過神經元做權重 $w$ 的計算後再加總後，中間直排的 $h=(H1, H2)$ 就會被向右輸出到最右直排的輸出層輸出 $y=(y1,y2)=(0.01, 0.99)$ ，左邊直排的神經元輸出就是右邊直排神經元的輸入，同一直排的神經元彼此間沒有聯繫，但和右邊的神經元會有聯繫，右邊的神經元也不會向左邊輸出，這是一個資料從左到右的流動過程且是單向不可逆的，這個過程就稱為正向傳遞。

反向傳遞 Backward Propagation

在我們經過正向傳遞輸出模型的預測值後，通常會再用損失函數去衡量預測值和實際結過之間的差距，計算模型預測的損失，然後會需要去最小化損失函數的值，若整個神經網路共有 3 個權重，這 3 個權重也可視為模型的參數，損失函數就要對這些參數取偏導數計算梯度，用來應用在梯度下降的概念，也就是說用我們正向傳遞輸出的結果往回推，往回推指的就是在計算過程中會經過每層隱藏層，和正向傳遞的方向相反，由右至左傳遞。

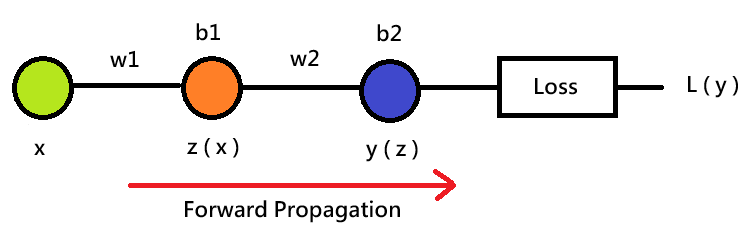
上面是包含一個隱藏層的神經網路，在不考慮激勵函數的情況下，計算方向 $x$ → $z$ → $y$ 、最後再透過 $y$ 算出損失函數 $L(w_1,w_2,b_1,b_2)$ ，求損失函數所經歷的由左至右計 ( 輸入層 → 隱藏層 → 輸出層 ) 計算過程，其實就是正向傳遞。

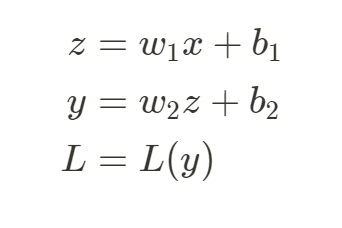
在算出損失函數後，我們會對參數 $w_1$ 、 $w_2$ 、 $b_1$ 、 $b_2$ 進行優化，也就是 $L(w_1,w_2,b_1,b_2)$ 損失函數分別對參數求偏導數做偏微分計算梯度， $L$ 若是單變數函數就用微分算其導數。

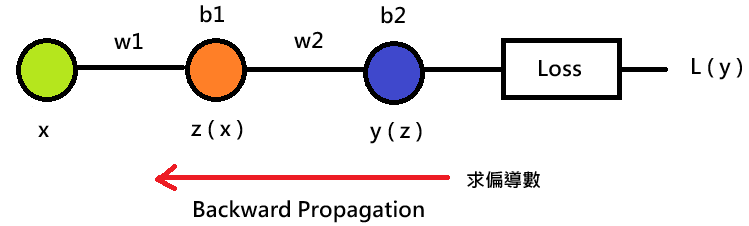
求梯度的過程會從 $L$ 回推到參數 $w_1$ 、 $w_2$ 、 $b_1$ 、 $b_2$ ，這會運用到微積分中連鎖率 ( Chain Rule ) 的概念，會發對 $w_1$ 偏微分時，因為連鎖率的特性，會從最右邊的輸出層 $y$ 經過隱藏層 $z$ 往回計算到最左邊的輸入層 $x$ ，每經過一層就會做梯度的相乘，和正向傳遞計算的方向相反，這個過程就叫反向傳遞，這邊也要注意，因為梯度相乘，所以可能會有梯度爆炸或是梯度消失的問題發生，詳細部分我們下次再來說明。

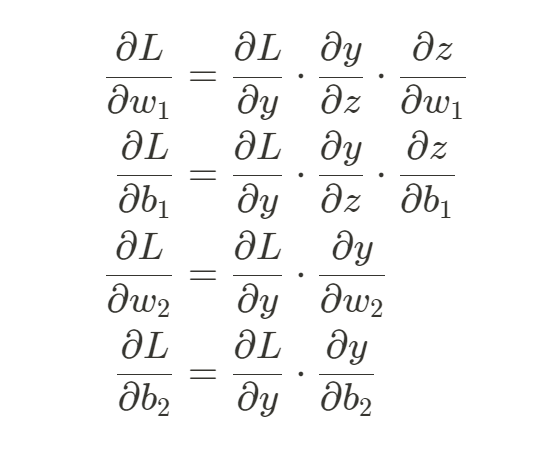
對每個參數計算完偏微分後就可以得到所有參數的梯度 $\nabla{L}$ ，用來做參數的優化。

參數優化

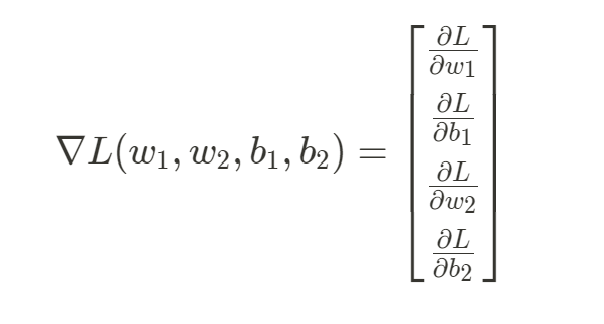
模型的訓練過程其實就是透過不斷地進行正向傳遞與反向傳遞來優化參數，在每次訓練時的迭代中，先給定一個初始參數，用參數去進行正向傳遞算出損失函數 $L$ ( 正向傳遞 )後，算出參數在損失函數的梯度 $\nabla{L}$ ( 反向傳遞 )，接著利用梯度 $\nabla{L}$ 和原本參數進行計算後得到更新後的參數，最後用更新後的參數取代原本參數，完成參數更新的流程，在理想情況中，更新後的參數會比原來的參數的損失函數值更小，梯度取絕對值也變小，每次更新就往損失函數的全局最小值處接近一步。

隨著每次迭代參數就不斷地在優化，這過程也稱作梯度下降 ( Gradient Descent )，根據迭代次數不斷更新參數直到滿足訓練停止條件 ( 訓練到達迭代次數或是梯度為 0，參數值不再更動 ) 後，此時的參數就是模型優化的最佳解。